8 Estratégias de Sudoku para principiantes explicadas

O Sudoku pode parecer um jogo fácil, dado as suas regras simples e claras, mas está pensado para ser sempre desafiante em qualquer nível. Qualquer novo jogador deverá, por isso, estar preparado para se debater com dificuldades e dúvidas durante a resolução destes puzzles. Felizmente, existem estratégias de Sudoku para principiantes que ajudam o podem ajudar a progredir mais facilmente no jogo e a entender a dinâmica da tabela.
1. Análise cruzada
A análise cruzada é normalmente a primeira estratégia utilizada nas tabelas de Sudoku.
O jogador deve começar por focar a sua atenção nos grupos de 3 x 3 e detectar quais os números em falta nestes. O passo seguinte será tomar cada dígito individualmente e cruzar a informação já presente nas colunas e linhas ligadas ao grupo em análise.
Exemplo
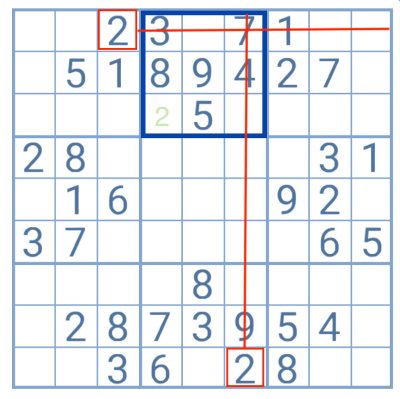
No grupo destacado existem três quadrículas em branco que terão de ser preenchidas com os números que estão em falta (1, 2, 6).
Duas das linhas ligadas a este grupo contêm o número 1. Ao cruzar esta informação, o jogador pode definir este dígito como candidato a duas células, das três vazias. O número 6 está presente numa das colunas que une ao grupo, mas também aqui é só possível reduzir o seu posicionamento a duas possibilidades.
No entanto, ao testar o número 2, o jogador descobre apenas uma solução possível para este dígito e pode adicioná-lo com confiança à tabela.
Nota: Ainda que não faça parte necessariamente das estratégias de Sudoku para principiantes, estar atento à evolução da tabela é um requisito neste jogo.
Neste exemplo, o número 2 ocupou uma das duas posições para a qual o número 1 era candidato, ou seja, o jogador encontrou assim a solução também para este dígito. Por exclusão de partes, a última quadrícula será preenchida com o 6. O número 2 desbloqueou assim a solução para o grupo destacado.
2. Contagem
A contagem é uma estratégia muito útil quando na tabela existe uma coluna ou linha parcialmente preenchida e com apenas 2 ou 3 quadrículas em branco.
Uma vez que não podem existir repetições por linha ou coluna, o jogador terá apenas de contar os números já posicionados para descobrir quais as incógnitas e anotar esses dígitos como candidatos às células vazias. O passo seguinte será utilizar a análise cruzada para tentar encontrar a solução.
Exemplo
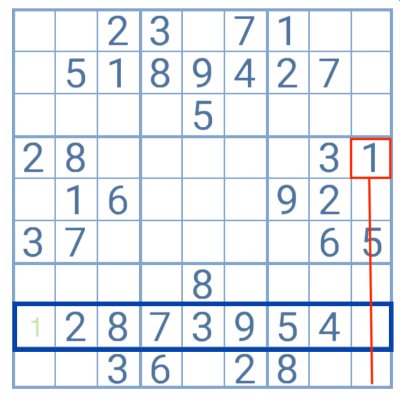
O 1 e o 6 são os únicos dígitos em falta na linha destacada, pelo que podem ser anotados como candidatos às casas em branco.
No entanto, ao cruzar a informação das colunas com as quais essas células interceptam é possível verificar que o número 1 tem apenas uma possibilidade de colocação. O jogador terá assim encontrado a solução para esta linha.
3. Único solitário
Os únicos solitários apresentam uma grande incidência no nível fácil, o que a torna numa das estratégias de Sudoku para principiantes mais úteis nesta fase.
Para aplicá-la, o jogador deve apontar todos os candidatos a cada quadrícula. Começar pelos grupos individualmente é um bom método para tornar o processo mais rápido. Se depois de anotados todos os dígitos, o jogador encontra uma quadrícula com apenas um candidato isolado (único solitário), estará perante a sua solução.
Exemplo
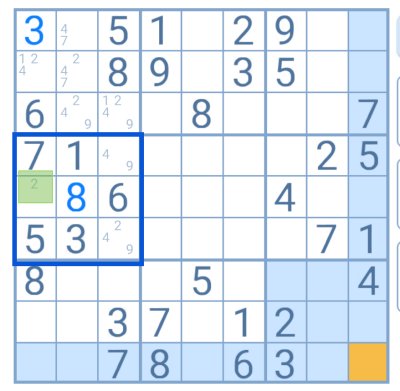
Este puzzle de Sudoku ainda está no início e restam muitas incógnitas e espaços por resolver.
No grupo destacado, pode ver-se que o número 2 é candidato em duas células e que é impossível determinar a sua solução apenas cruzando a informação das linhas e colunas.
No entanto, depois de anotados todos os candidatos nesse grupo, é possível encontrar uma casa na qual o 2 é a única possibilidade. Neste caso, o jogador encontrou um único solitário e já pode posicionar esse dígito na tabela.
4. Único oculto
Ao passo que com um único solitário existe apenas um candidato para uma quadrícula, com o único oculto o jogador encontra um dígito com apenas uma posição possível, ainda que esteja acompanhado de outros candidatos para a mesma célula.
O jogador pode então remover os demais candidatos e posicionar o dígito solitário.
Exemplo
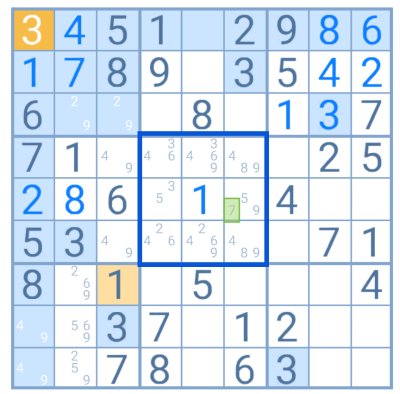
Neste exemplo, o número 7 é candidato a apenas uma quadrícula dentro do grupo destacado. Essa será a sua solução. Diz-se “oculto” porque partilha essa célula com outros candidatos, neste caso o 5 e o 9, o que torna mais difícil encontrá-lo.
5. Pares solitários
Os pares são um grupo de estratégias de resolução de Sudokus que ajudam o jogador a reduzir o número de candidatos nas quadrículas, mas não revelam a solução final.
Os pares solitários são os mais simples e fáceis de encontrar. Ocorrem quando duas células, na mesma coluna ou linha, partilham o mesmo par de candidatos isolados. O jogador não sabe ainda qual a solução para cada dígito, mas já consegue determinar a sua posição geral dentro da tabela. Assim, pode eliminar esses números como candidatos a outras quadrículas na mesma linha ou coluna.
Exemplo
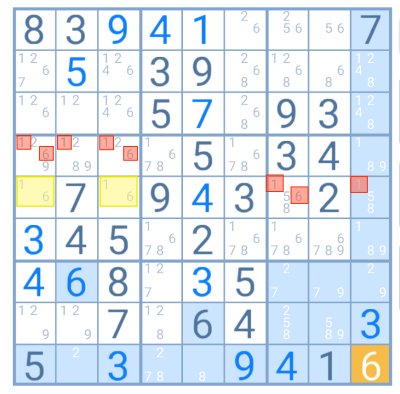
Neste exemplo, o par solitário está destacado a amarelo. O jogador sabe que o 1 e o 6 estarão seguramente nessas casas, mas não conhece ainda a solução. Contudo, pode já eliminar estes dígitos como candidatos a outras células nessa linha e no próprio grupo (dígitos destacados a vermelho).
6. Pares ocultos
Os pares ocultos ocorrem em grupos de 3 x 3, quando existem duas quadrículas com o mesmo par de candidatos e nenhum desses dígitos é candidato a outras casas desse grupo. Assim, o jogador consegue identificar que essa será a sua posição final e pode eliminar os demais candidatos presentes nessas quadrículas.
Exemplo
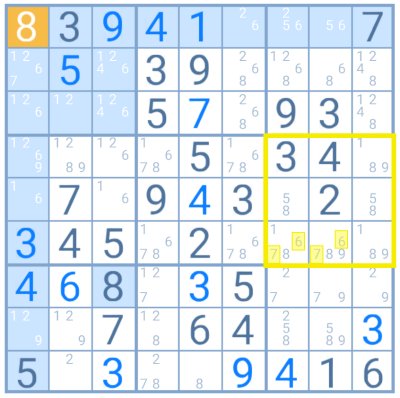
No grupo destacado, o 6 e o 7 são candidatos em apenas duas células e formam um par. O jogador pode eliminar os demais candidatos nessas casas (7, 8 e 9).
Uma vez que as quadrículas deste par estão posicionadas na mesma linha, o resultado será um par solitário. No entanto, esta é apenas uma coincidência, já que os pares ocultos podem estar posicionados aleatoriamente dentro do grupo.
7. Triplos solitários
Os triplos solitários são conjuntos de pares (a/b - a/b) ou triplos (a/b/c - a/b/c) iguais, presentes em três células diferentes numa mesma linha ou coluna. Não podem existir mais candidatos nessas células.
O jogador pode então assumir que a solução final para esses dígitos estará nessas quadrículas e eliminá-los como candidatos a outras células nessa linha ou coluna.
Exemplo
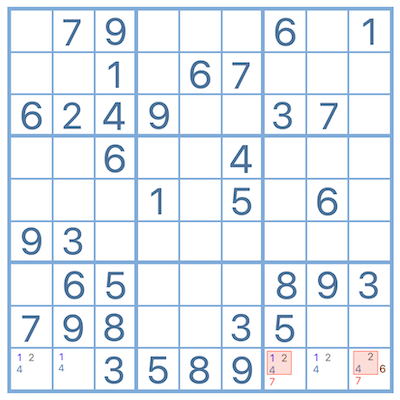
Neste exemplo, o jogador tem uma linha com três células contendo três números idênticos (1/2/4). Não há outros números possíveis para essas células. Isto significa que colocar um dígito numa delas afetará diretamente as duas restantes e forçará a sua solução.
Por exemplo, se o jogador colocar o 1 ou o 4 na primeira célula da linha, a segunda célula ficará com um Único Solitário que por sua vez deixará a terceira célula com o número 2 também como um Único Solitário.
Se o jogador colocar o 2 como solução para a primeira célula, então as outras duas ficarão com Pares Solitários (1-4).
Portanto, independente da situação, os dígitos deste conjunto (1/2/4) podem ser eliminados como possibilidades para as demais células daquela linha.
8. Triplos fechados
Tanto os triplos solitários como os triplos fechados são estratégias de Sudoku para principiantes muito similares. A única diferença entre estas é que a primeira apenas se aplica em linhas e colunas, ao passo que que a última ocorre apenas em grupos.
O princípio é o mesmo nos dois casos. Se o jogador encontra três quadrículas com dois ou três candidatos iguais e isolados, pode remover esses dígitos como possibilidades a outras células desse grupo.
Exemplo
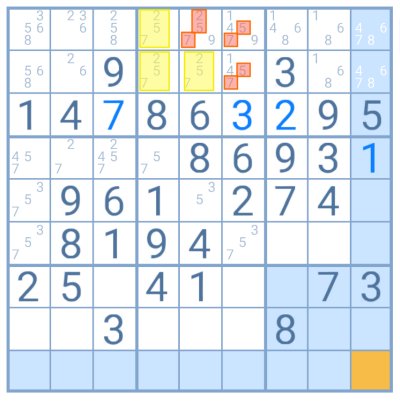
Neste exemplo, o jogador encontrou três casas dentro de um grupo com os mesmos três candidatos (2/5/7). Ao utilizar o método dos triplos fechados, pode eliminar esses dígitos como candidatos a outras células do grupo (aqui marcados a vermelho).
Estas estratégias de Sudoku para principiantes são muito úteis para qualquer jogador que se proponha a enfrentar os desafios destes puzzles pela primeira vez. Com a prática, estas técnicas ficaram alojadas na mente do jogador que rapidamente as estará a aplicar de forma automática e sem pensar. São o primeiro passo no caminho para se tornar um jogador avançado e dominar até os níveis mais difíceis deste quebra-cabeças numérico.












