6 Técnicas de resolución de sudoku avanzadas

Las técnicas de resolución de Sudoku avanzadas son utilizadas en los niveles más difíciles y su objetivo puede ser la eliminación de candidatos o encontrar la solución para una celda específica. Sea cual sea el caso, su aplicación exige siempre altos niveles de concentración ya que funcionan por deducción.

1. Técnica X-Wing

La estrategia X-Wing es una de las técnicas de resolución de Sudoku avanzadas más básicas. También puede ser aplicada en niveles intermedios, aunque su incidencia es muy reducida en estos casos. Su objetivo es eliminar candidatos.

El jugador puede utilizar esta técnica cuando existe un candidato repetido en cuatro celdas que forman un cuadrado o rectángulo cuando unidas mentalmente por columna o línea. Al trazar una X que une diagonalmente las extremidades de esta forma geométrica, es posible verificar que existen solamente dos pares de posiciones posibles para ese dígito.

El paso siguiente será probar cada uno de los pares en la tabla y eliminar ese número de cualquier celda que se vuelva imposible en ambos los casos.

Ejemplo

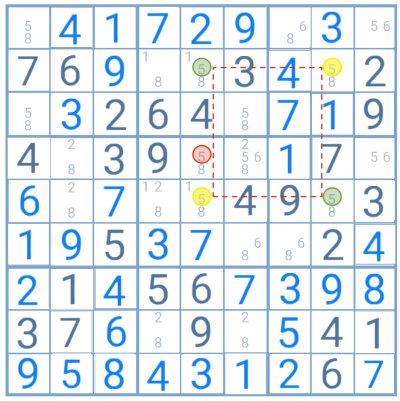
En este ejemplo, el número 5 forma la configuración necesaria para la aplicación de la técnica X-Wing. Al conectar las células con ese dígito, se puede ver con facilidad que solo los pares destacados en verde o en amarillo serían posibles en esta situación ya que uno invalida al otro.

Al probar los dos pares en la tabla, el número 5, destacado en rojo, resulta como imposible en ambos casos. Por lo tanto, puede ser eliminado como candidato en esa celda.

2. Técnica Swordfish

Igual que con la estrategia X-Wing, también la Swordfish ayuda a eliminar candidatos en las celdas.

Para aplicarla, el jugador debe encontrar un dígito candidato en dos celdas en una misma línea, en tres líneas distintas. Estas cuadrículas deben también estar unidas por columna, independientemente de la forma geométrica que diseñen.

Al conectar estas celdas, el resultado será una cadena cerrada en la cual solo dos conjuntos de posiciones son posibles para ese dígito. El jugador debe probarlos y eliminar ese número como candidato en cualquier celda que se vuelva imposible cuando los dos conjuntos son aplicados.

Ejemplo

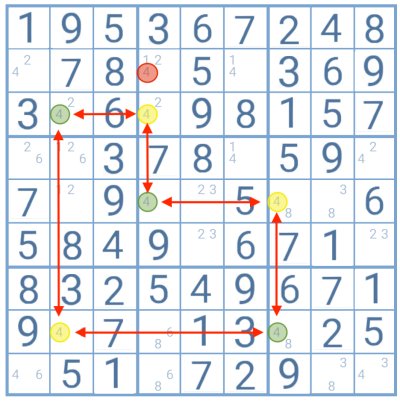
En esta tabla, el número 4 es candidato en dos celdas, en tres líneas diferentes, lo que permite la utilización de la técnica Swordfish.

Cuando conectadas, se puede verificar que siempre que uno de los dígitos destacados en verde es posible, aquellos en amarillo se vuelven imposibles y viceversa. Así, existen solamente dos posibilidades en esta cadena con el número 4, el conjunto en verde o el conjunto en amarillo.

Al aplicar los dos en la tabla, el jugador descubre que el 4 destacado en rojo sería imposible como candidato en esa celda en ambos los casos. Puede, por eso, ser eliminado, dejando los dígitos 1 y 2 como únicos candidatos en esa cuadrícula.

3. Cadenas forzadas

Las cadenas forzadas son una de las técnicas de resolución de Sudoku avanzadas más fáciles de entender. Desafortunadamente, aplicarlas exige altos niveles de concentración y su resultado puede ser incierto. Cuando funcionan, el jugador descubre la solución para una celda.

Para poder aplicar la técnica de las cadenas forzadas deben existir en la tabla cuadrículas con solamente dos candidatos. El jugador debe elegir una y probar cómo evoluciona la tabla cuando cada dígito de esa celda es aplicado. El objetivo de esta técnica es encontrar una casilla en la cual la solución es siempre la misma, independientemente del dígito inicial elegido. En este caso, esa será la solución final para esa casilla.

Ejemplo

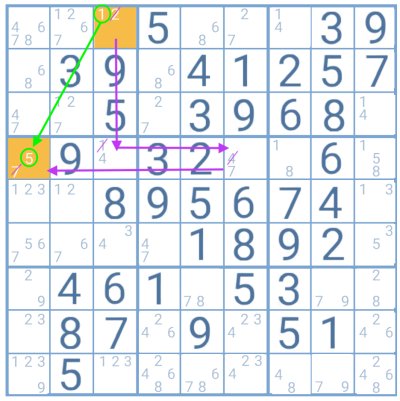
En este ejemplo, el jugador ha elegido la celda destacada en el tope de la tabla, con los candidatos 1 y 2, para probar la técnica de las cadenas forzadas. Tanto el uso del número 1 como del número 2 producen siempre el mismo resultado en la segunda celda destacada (con el 5 y el 7), el número 5. Así, el jugador puede ya apuntar este dígito como la solución en esa casilla.

Hay que notar que, al probar el número 1, el jugador podría también iniciar la cadena en dirección al lado derecho, para la celda con el 1 y el 4 como candidatos. Este camino sería más largo, pero el 5 continuaría siendo la solución en la cuadrícula destacada.

De todas las técnicas de resolución de Sudoku avanzadas, las cadenas forzadas suelen ser de las más evitadas por los jugadores ya que sus cadenas pueden ser bastante largas y no siempre producen los resultados deseados.

4. Técnica XY-Wing

La técnica XY-Wing es utilizada para eliminar candidatos. Puede ser aplicada cuando hay tres celdas en la tabla con solo un par de candidatos y estas comparten por lo menos un dígito entre sí (p.ej. AB/AC/CB). Con alguna imaginación, estas celdas crean la forma de una Y, en la que una toma el lugar de base o tallo y las demás son los ramos. Cada ramo debe compartir un dígito con el tallo.

El jugador debe entonces imaginar un rectángulo o cuadrado sobre estas celdas, en el que cada una será una extremidad. La cuarta será la intersección entre los ramos. Si a lo largo de las líneas que unen las extremidades o en la celda de intersección hay un candidato compartido por estas, entonces puede ser eliminado.

Ejemplo

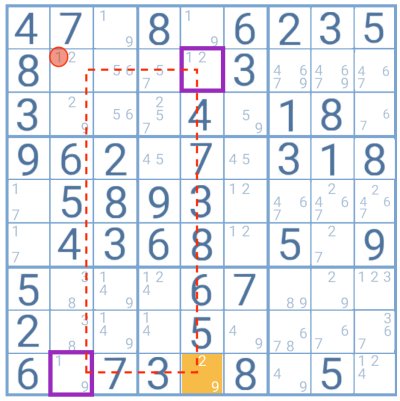
En este ejemplo, la celda base o tallo (destacada en naranja) contiene los candidatos 2 y 9 y está conectada a los ramos destacados en morado, con los cuales comparten un dígito.

Si alguna de las cuadrículas cruzadas por la línea roja tuviera ese candidato compartido por el ramo y el tallo, este podría ser eliminado; sin embargo, no es el caso en esta situación.

Sin embargo, la celda de intersección entre los ramos comparte un candidato con estos, el número 1, lo que permite al jugador eliminarlo de esa casilla.

5. Rectángulo de unicidad

Los puzles de Sudoku solo pueden tener una solución. Sin embargo, en los niveles de dificultad más avanzados, es posible que el jugador encuentre dos. Esta situación ocurre cuando existe un patrón de unicidad, es decir, cuatro celdas con pares de candidatos iguales frente a frente y en grupos concurrentes. En este caso, hay dos posibles soluciones para cada casilla ya que la elección de los dígitos es aleatoria.

Para evitar múltiples soluciones es necesario aplicar la estrategia del rectángulo de unicidad. Durante el juego, siempre que surja la perspectiva de un patrón de unicidad en el final del puzle, el jugador debe verificar si existen otros candidatos en alguna de esas cuatro casillas. En el caso de una respuesta positiva, el jugador debe eliminar los “dígitos problemáticos” y mantener los demás candidatos en esa celda.

Ejemplo

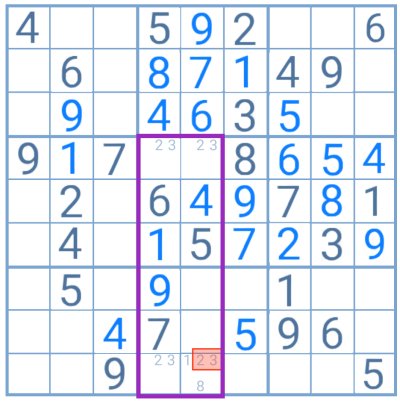
En esta tabla, el jugador está frente a una fuerte posibilidad de encontrar un patrón de unicidad en el final del puzle, gracias a las cuadrículas con los candidatos 3 y 4. Sin embargo, el 8 es también candidato en una de estas. Luego, al aplicar el rectángulo de unicidad, el jugador puede eliminar el par 3/4 y mantener el 8 como candidato en esa celda.

En teoría, la estrategia del rectángulo de unicidad es (o debería ser) la menos utilizada de todas las técnicas de resolución de Sudoku avanzadas ya que el patrón de unicidad solo ocurre en puzles mal formulados, aunque no totalmente errados.

6. Nishio

De todas las técnicas de resolución de Sudoku avanzadas, esta es usualmente utilizada como último recurso ya que su premisa implica cierto grado de adivinanza.

La técnica es muy sencilla. El jugador debe seleccionar una casilla con solamente dos candidatos, elegir uno de ellos e intentar solucionar la tabla. Si lo logra, perfecto. Si no, tendrá que volver al punto de partida y elegir el otro dígito.

La idea por detrás de esta técnica es clara. En el momento en que el jugador encuentra una incompatibilidad, puede eliminar ese dígito, encontrando así la solución para la celda en el punto de partida.

Sin embargo, es muy fácil equivocarse por falta de concentración y volver el puzle imposible con esta estrategia. Además, la incompatibilidad puede surgir solamente al final. Por estas razones, la mayoría de los jugadores prefiere evitar utilizar esta estrategia.
 

La teoría por detrás de las técnicas de resolución de Sudoku avanzadas es relativamente fácil de entender y de aplicar. Lo complicado es encontrar las configuraciones correctas y saber qué técnica utilizar en cada caso. Sin embargo, cualquier jugador que desee afrontar los niveles de Sudoku más difíciles tendrá que estar bien familiarizado con estas estrategias, ya que estas se vuelven en imprescindibles para solucionar los puzles en esos niveles.